Pentagon unit

(Click for bigger image)
The dodecahedron is made from 12 pentagons. The pentagons can be made as follows. They are not exact pentagons, but they are close enough to make an origami dodecahedron.
Start with a square of paper. The first step is to fold the paper into thirds. You can use your favourite method. In this example, (a mathematicians method) the two diagonals folded in the first picture intersect at a third along, and a third up the paper.

Here's another way to fold a sheet of paper into thirds, which I learnt from the origami-l mailing list.
You take your paper you want to fold in thirds, and some lined paper:
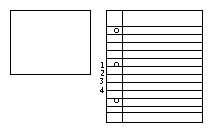
You think about four equally spaced lines, 1,2,3,4, and put one corner of the paper you want to fold on line 1, and one on line 4:
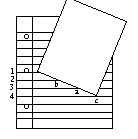
Then you fold so the corner c touches b, and fold along from a:
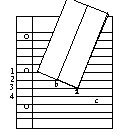
Then fold along from b to get paper divided nicely into thirds.
Anyway, suppose you've got your paper divided into three.
Next, fold over triangles of sides 1 and 1/3, as below. Then fold over the other corners along the lines made by the first triangles folded over. Then fold the whole thing in half. The angle at the top is pretty close to 108 degrees. It's not exact, but this is just a poor man's pentagon. (what you do get, is that since you folded a third of the paper, there's an angle that's arctan(3), which is pretty close to 72, and the angle at the top is 180-arctan(3).) (Well, there's another problem that the sides of this diamond shaped thing might not be quite all equal; but they are pretty close.)

Then you have to fold over the long pointy parts to make a pentagon shape. There are creases you can match the points up with that give reasonable side lengths. (ie, the lines that divided the paper into three; they give lines from the points to a point on the opposite side to fold to.)

Finally, to make things a bit more secure, open it out a little; now you want to slip flap "a" underflap "b"; you do this while bringing the two points labeled "c" together, and this makes them stay together better.
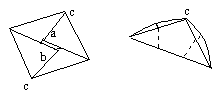
That's the pentagon done now. All you have to do is make 12, and fit them all together by putting the pointy bits into the slots created along the upper two edges of the pentagon.
Note that there is one edge that is niether a point nor a slot; you'll get 12 of these in the total dodecahedron, and you should make sure they match up in 6 pairs.
Note, if you use the ruled paper method, and only make one of the third creases, and then use the folded over edge of that one side of paper to mark where to fold from, you will end up with a pentagon with no creases on one side, and so you get a pretty neat dodecahedron.
Home