Perimeter problem

The problem is, can you fold a piece of paper somehow so that the area of the perimeter of the resulting flat shape is bigger than the original area.

The answer is yes, but this is not obvious, especially if you've not done much origami.

I learnt of this problem on the origami mailing list.

Since several of my mathematician, but non origami, friends were interested in this, I decided to write up a solution which was also given on the origami mailing list, by origamist Robert Lang.

So, the following is not due to me, and I don't know of how to construct other models that have this property, but if I find any, I shall add them here too.

(Note, recently a method of increasing the perimeter of a rectangle (dollar bill) was given in 'the Mathematical Intellegencer'; the method shown there is different from this method; the method below can also be generalized to apply to rectangles; and also can be combined with the method of the Inteligencer article. Also Robert Lang has a method of folding a square or rectangle to create arbitrarily large perimeter - though in practice paper thickness will probably mean that that construction is not going to increase the perimeter by massive amounts, but I have not tried folding it yet. Unfortunately I do not currently have enough time to write further details about all the above.)

Another reference for this problem is http://www.ics.uci.edu/~eppstein/junkyard/napkin.html.

Construction

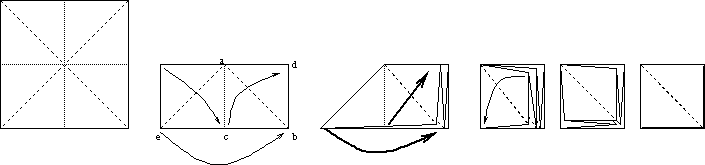
You begin with making a standard origami base, the first set of figures below show how to do this:

Once you have the base, you follow the next set of diagrams:

Calculation

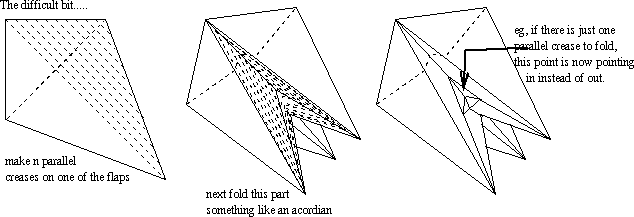
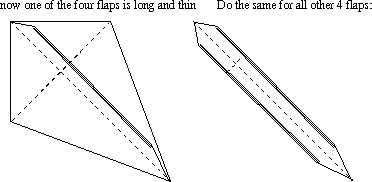
Here's the check that this figure really does have perimeter bigger than 4, if 4 was the original perimeter of the square before folding began.

Want to label some lengths:

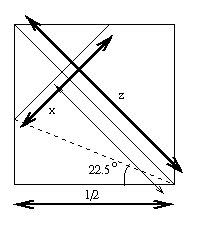
For simplicity, I'll take n=8, so the width w of the "fingers" of this figure are an eighth of the original width, which was x/2=(root(2)-1)/2.

• The downwards fingers are length 1/2, so have perimeter about 1 each (just a little bit more.
• The sideways fingers have length 1/2-3w, so a perimeter of a little more than 1-6w each.
• The part at the top has height x/2-w, so perimeter a little more than x-2w.

So the total perimeter is 2+2(1-6w)+x-2w=4+x-14w.

But w=x/16, so this is 4+x-14/16x=4+1/8x.

If we had n folds, then we'd get perimeter

As n tends to infinity, this gets closer and closer to 4+x, which is about 4.4

Crease diagrams

Here are some crease diagrams for several of the above steps. Unfortunately they still need some more work. I am going to prepare a method so I can avoid having to do all the crease pattern, and show this thing really does work!

This is the crease diagram for the bird base before the legs get thinned out.

This is the crease diagram for the model after the legs are thinned out:

This is after the front two arms are lifted up:

This is after the lower two legs are parted slightly:

These diagrams may be improved when I have time. (But probably not!)

Simplifications to argument

Look at the second of the above crease diagrams.

Take just one eightth of the paper:

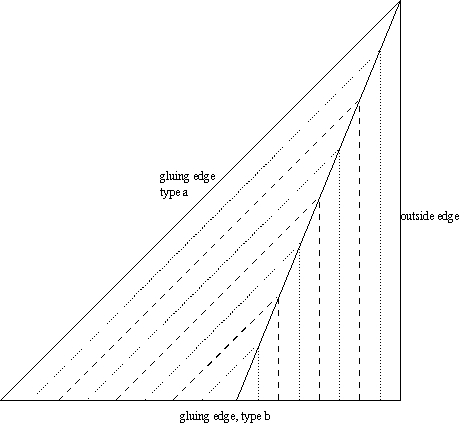
There are 8 things like this, the same up to reflection (and rotation etc).

This is what they look like when folded:

Note, if you like straight lines better, we can do a little more folding to make the edges to be glued all lie on a straight line:

Here is a kind of gluing diagram:

Next we want to look at necessary folding of each leg.... left as exercise for reader for now.